Momentum Contrast (MoCo)

Understanding Momentum Contrastive Learning for Unsupervised Visual Representation Learning

Introduction

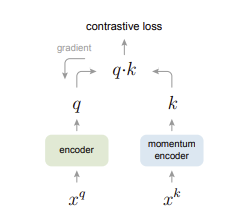
MoCo (Momentum Contrast) is a self-supervised learning framework introduced by Facebook AI Research in 2019. It addresses the fundamental challenge of learning visual representations without labeled data by treating contrastive learning as a dictionary look-up problem.

The key insight behind MoCo is that contrastive learning can be viewed as training an encoder to perform a dictionary look-up task, where we want to match a query representation with its corresponding key.

Note

Read the original paper: He, Kaiming, et al.
Momentum Contrast for Unsupervised Visual Representation Learning (MoCo) (2019)
arXiv:1911.05722

Core Concepts of MoCo

1. Dictionary Look-up Perspective

MoCo (Momentum Contrast) reframes contrastive learning as a dictionary look-up task:

• Query (q): An encoded representation of an augmented image.
• Positive Key (k⁺): The encoded representation of a different augmentation of the same image as the query.
• Negative Keys (k⁻): Encoded representations of different images.
• Dictionary: A dynamic set of keys (representations) used to compare against the query. The goal is to bring the query closer to its positive key while pushing it away from negative keys.

2. Queue Mechanism

MoCo introduces a queue-based dictionary to efficiently manage a large set of negative samples:

• A FIFO queue stores encoded representations (keys) from previous mini-batches.
• As new keys are added to the queue, the oldest keys are removed.
• This design ensures:
  • A large and consistent dictionary size independent of the mini-batch size.
  • Better utilization of past samples, improving contrastive learning.

3. Momentum Update

Instead of training both encoders via backpropagation, MoCo stabilizes learning with a momentum update for the key encoder:

• Query Encoder (f_q): Updated normally using gradient descent.

• Key Encoder (f_k): Updated as an exponential moving average of the query encoder:

  \[ \theta_k \leftarrow m \cdot \theta_k + (1 - m) \cdot \theta_q \]

• Momentum Coefficient (m): Typically set to 0.999, ensuring slow, stable updates.

This strategy helps maintain consistent representations for keys, reducing noise in the contrastive learning process.

MoCo Architecture and Algorithm

Architecture Components

• Query Encoder (f_q): A CNN (typically ResNet) that encodes query images.
• Key Encoder (f_k): A CNN with identical architecture to f_q, updated via momentum.
• Queue: A memory bank storing encoded keys from previous batches.
• Projection Head: An MLP that projects features into a lower-dimensional embedding space.

Training Process

1. Sample a mini-batch of N images.

2. Apply data augmentation to each image to create query and key views.

3. Encode queries using f_q and keys using f_k.

4. Compute the contrastive loss between each query and all keys in the queue.

5. Update the query encoder (f_q) via gradient descent.

6. Update the key encoder (f_k) via momentum update:

   \[ \theta_k \leftarrow m \cdot \theta_k + (1 - m) \cdot \theta_q \]

7. Update the queue by enqueuing the new keys and dequeuing the oldest keys.

InfoNCE Loss

MoCo uses the InfoNCE (Noise Contrastive Estimation) loss:

\[ \mathcal{L}_q = -\log \left( \frac{\exp(q \cdot k^+ / \tau)}{\sum_i \exp(q \cdot k_i / \tau)} \right) \]

Where:

• \(q\): Query representation
  
• \(k^+\): Positive key representation
  
• \(k_i\): All keys in the dictionary (including positive and negatives)
  
• \(\tau\): Temperature parameter
  
• \(\cdot\): Dot product (cosine similarity after L2 normalization)

MoCo Architecture

# MoCo Implementation in PyTorch
import torch
import torch.nn as nn
import torch.nn.functional as F

class MoCo(nn.Module):
    def __init__(self, base_encoder, dim=128, K=65536, m=0.999, T=0.07):
        """
        MoCo: Momentum Contrast for Unsupervised Visual Representation Learning

        Args:
            base_encoder: backbone CNN architecture (ResNet)
            dim: feature dimension for contrastive learning
            K: queue size (number of negative samples)
            m: momentum coefficient for key encoder update
            T: temperature parameter for InfoNCE loss
        """
        super(MoCo, self).__init__()
        self.K = K
        self.m = m
        self.T = T

        # Create query and key encoders
        self.encoder_q = base_encoder(num_classes=dim)
        self.encoder_k = base_encoder(num_classes=dim)

        # Initialize key encoder parameters with query encoder
        for param_q, param_k in zip(self.encoder_q.parameters(), self.encoder_k.parameters()):
            param_k.data.copy_(param_q.data)
            param_k.requires_grad = False  # Key encoder is not updated by gradient

        # Create the queue for storing keys
        self.register_buffer("queue", torch.randn(dim, K))
        self.queue = nn.functional.normalize(self.queue, dim=0)

        # Queue pointer for circular buffer
        self.register_buffer("queue_ptr", torch.zeros(1, dtype=torch.long))

    @torch.no_grad()
    def _momentum_update_key_encoder(self):
        """
        Momentum update of the key encoder

        """
        for param_q, param_k in zip(self.encoder_q.parameters(), self.encoder_k.parameters()):
            param_k.data = param_k.data * self.m + param_q.data * (1. - self.m)

    @torch.no_grad()
    def _dequeue_and_enqueue(self, keys):
        """
        Update the queue by dequeuing old keys and enqueuing new keys
        """
        batch_size = keys.shape[0]
        ptr = int(self.queue_ptr)
        assert self.K % batch_size == 0
        self.queue[:, ptr:ptr + batch_size] = keys.transpose(0, 1)
        ptr = (ptr + batch_size) % self.K  # Move pointer
        self.queue_ptr[0] = ptr

    @torch.no_grad()
    def _batch_shuffle_ddp(self, x):
        """
        Batch shuffle for distributed training
        This prevents information leakage between query and key encoders
        """
        batch_size_this = x.shape[0]
        x_gather = concat_all_gather(x)
        batch_size_all = x_gather.shape[0]
        num_gpus = batch_size_all // batch_size_this
        idx_shuffle = torch.randperm(batch_size_all).cuda()
        torch.distributed.broadcast(idx_shuffle, src=0)
        idx_unshuffle = torch.argsort(idx_shuffle)
        gpu_idx = torch.distributed.get_rank()
        idx_this = idx_shuffle.view(num_gpus, -1)[gpu_idx]
        return x_gather[idx_this], idx_unshuffle

    @torch.no_grad()
    def _batch_unshuffle_ddp(self, x, idx_unshuffle):
        """
        Undo batch shuffle for distributed training
        """
        batch_size_this = x.shape[0]
        x_gather = concat_all_gather(x)
        batch_size_all = x_gather.shape[0]
        num_gpus = batch_size_all // batch_size_this
        gpu_idx = torch.distributed.get_rank()
        idx_this = idx_unshuffle.view(num_gpus, -1)[gpu_idx]
        return x_gather[idx_this]

    def forward(self, im_q, im_k):
        """
        Forward pass for MoCo

        Args:
            im_q: query images
            im_k: key images

        Returns:
            logits: logits for InfoNCE loss
            labels: labels for InfoNCE loss
        """
        # Compute query features
        q = self.encoder_q(im_q)  # queries: NxC
        q = nn.functional.normalize(q, dim=1)

        # Compute key features
        with torch.no_grad():  # No gradient for key encoder
            self._momentum_update_key_encoder()  # Update key encoder
            im_k, idx_unshuffle = self._batch_shuffle_ddp(im_k)
            k = self.encoder_k(im_k)  # keys: NxC
            k = nn.functional.normalize(k, dim=1)
            k = self._batch_unshuffle_ddp(k, idx_unshuffle)

        # Compute logits
        l_pos = torch.einsum('nc,nc->n', [q, k]).unsqueeze(-1)
        l_neg = torch.einsum('nc,ck->nk', [q, self.queue.clone().detach()])
        logits = torch.cat([l_pos, l_neg], dim=1)
        logits /= self.T
        labels = torch.zeros(logits.shape[0], dtype=torch.long).cuda()
        self._dequeue_and_enqueue(k)
        return logits, labels

# Utility function for distributed training
@torch.no_grad()
def concat_all_gather(tensor):
    """
    Performs all_gather operation on the provided tensors
    """
    tensors_gather = [torch.ones_like(tensor) for _ in range(torch.distributed.get_world_size())]
    torch.distributed.all_gather(tensors_gather, tensor, async_op=False)
    output = torch.cat(tensors_gather, dim=0)
    return output

Training Loop Implementation

# Example usage
def main():
    import torchvision.models as models

    # Create ResNet-50 base encoder
    def resnet50_encoder(num_classes=128):
        model = models.resnet50(pretrained=False)
        model.fc = nn.Sequential(
            nn.Linear(model.fc.in_features, model.fc.in_features),
            nn.ReLU(),
            nn.Linear(model.fc.in_features, num_classes)
        )
        return model

    # Initialize MoCo model
    model = MoCo(resnet50_encoder, dim=128, K=65536, m=0.999, T=0.07)

    # Setup optimizer 
    optimizer = torch.optim.SGD(model.parameters(), lr=0.03, momentum=0.9, weight_decay=1e-4)

    # Training loop
    for epoch in range(200):
        train_moco(model, train_loader, optimizer, epoch, device)
        # Add validation and checkpointing as needed

# Data augmentation typically used with MoCo
def get_moco_augmentation():
    from torchvision import transforms
    # MoCo v1 augmentation
    augmentation = transforms.Compose([
        transforms.RandomResizedCrop(224, scale=(0.2, 1.0)),
        transforms.RandomGrayscale(p=0.2),
        transforms.ColorJitter(0.4, 0.4, 0.4, 0.4),
        transforms.RandomHorizontalFlip(),
        transforms.ToTensor(),
        transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
    ])
    return augmentation

MoCo vs SimCLR

Aspect	MoCo	SimCLR
1. Dictionary Management	Queue-based dictionary with large, consistent size Independent of batch size Memory efficient	Uses within-batch negatives only Requires large batch sizes Memory intensive
2. Encoder Architecture	Two encoders: query (f_q) and key (f_k) Momentum update: \[\theta_k \leftarrow m \cdot \theta_k + (1 - m) \cdot \theta_q\] Asymmetric design	Single encoder for all samples Symmetric design No momentum update
3. Training Dynamics	Stable training with momentum Diverse negatives via queue Robust to batch size	Requires large batches All samples updated together More sensitive to batch size
4. Computational Requirements	Lower memory footprint Efficient for small batches Works on modest hardware	High memory requirements Needs multiple GPUs Heavy batch computations
5. Augmentation Strategy	Initially simple augmentations MoCo v2 adopts stronger ones Less dependent on augmentation	Strong augmentations essential Uses heavy transforms (blur, color distortions) Performance depends on augmentation strength

Summary and Practical Recommendations

When to Choose MoCo:

• Limited computational resources
• Suitable for academic research or prototyping environments
• Preferred when stable training is important
• Flexible with varying batch sizes
• Enables faster experimentation cycles

When to Choose SimCLR:

• Abundant computational resources
• Ideal for production environments with large-scale data
• Needed when maximum performance is a priority
• Well-suited for large-scale industrial applications
• Works best when strong augmentation pipelines are already established

Key Takeaways:

1. MoCo democratizes contrastive learning by making it accessible with limited resources
   
2. SimCLR achieves strong performance but requires significant computational investment
   
3. The two methods are complementary, serving different use cases
   
4. MoCo’s queue mechanism is an efficient solution to the negative sampling problem
   
5. SimCLR’s simplicity makes it easier to understand and adapt to specific applications

The choice between MoCo and SimCLR depends on your available resources and performance needs. MoCo strikes a practical balance between efficiency and effectiveness, while SimCLR excels when compute and scale are not limiting factors.